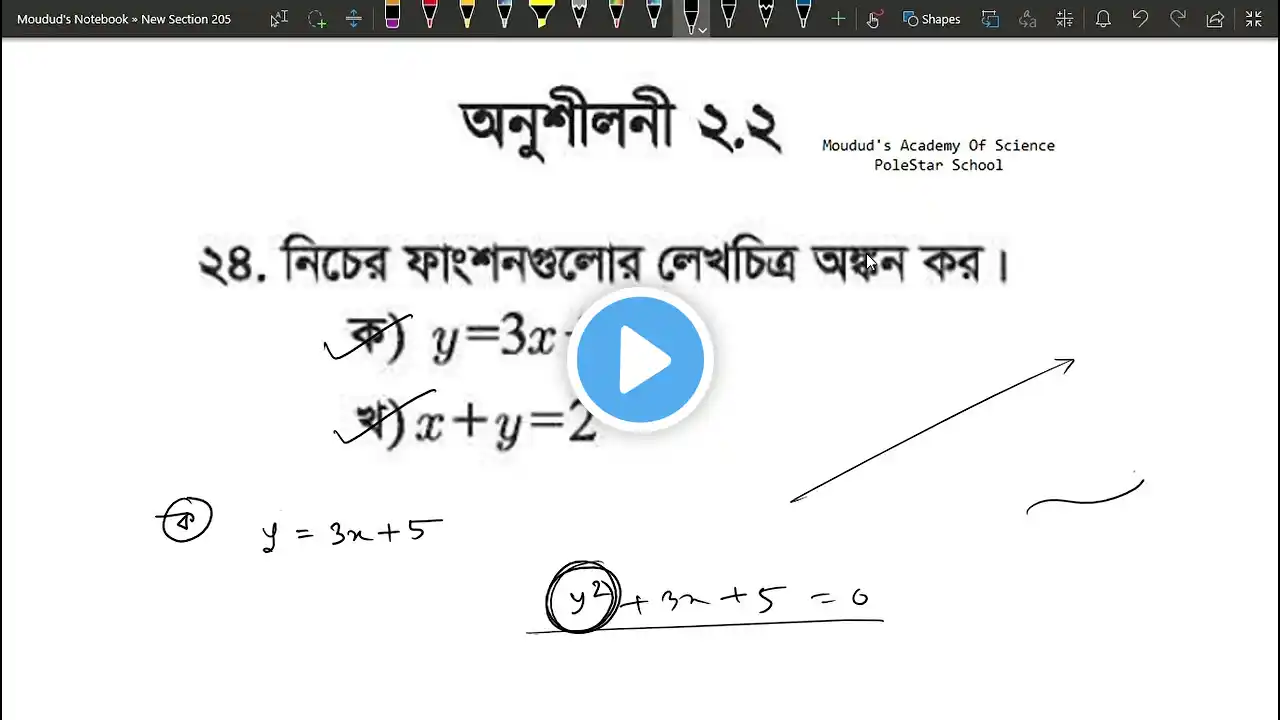
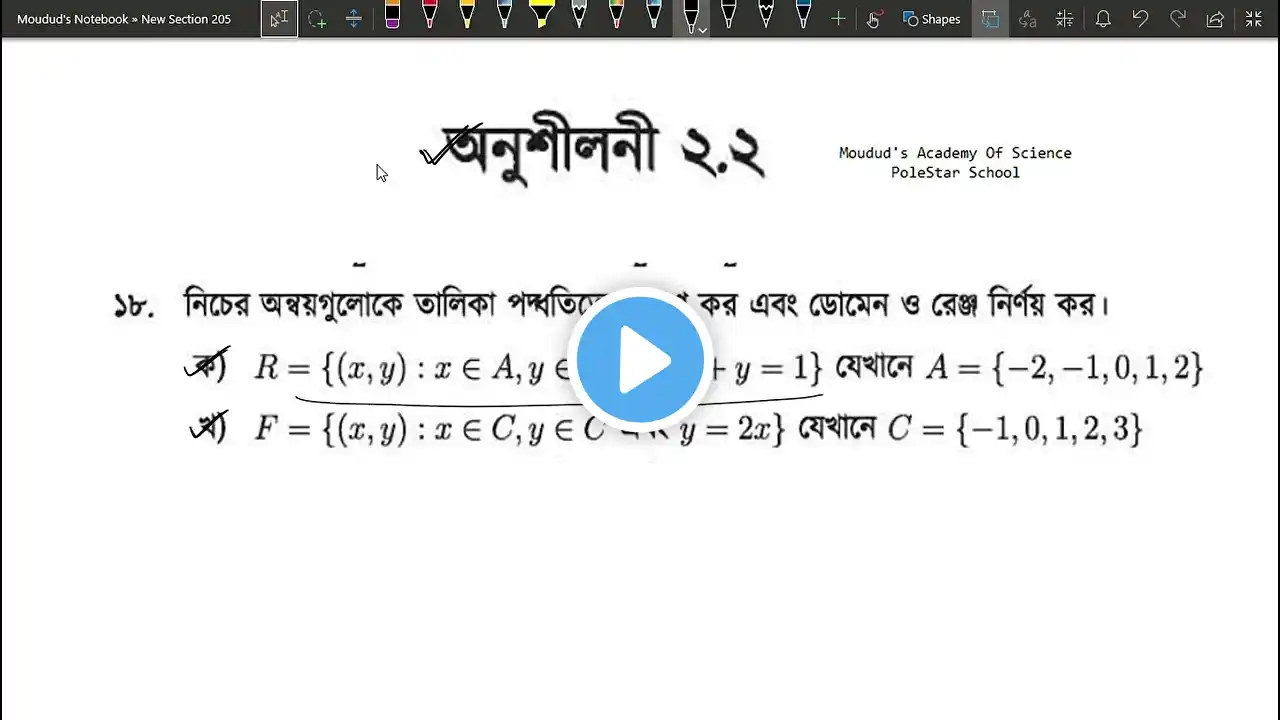
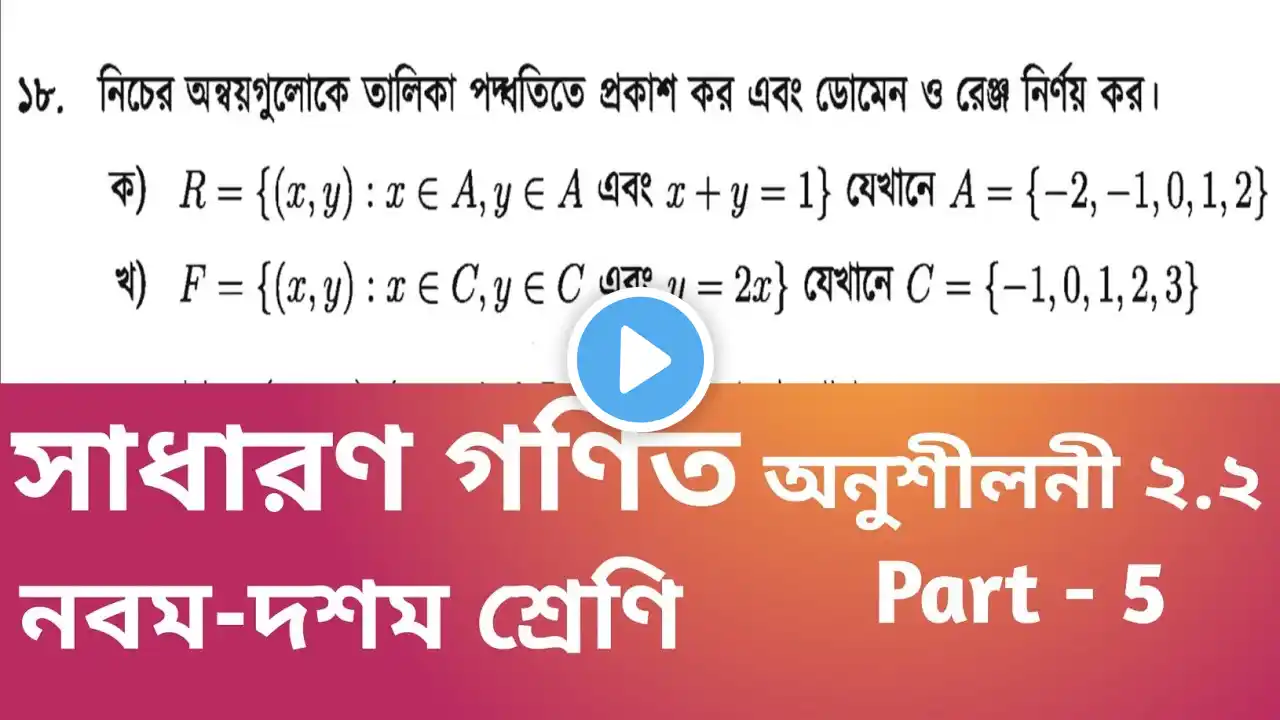
নবম দশম শ্রেণির গণিত অনুশীলনী ২.২ এর ১২,১৩,১৪ ও ১৫ নং প্রশ্নের সমাধান। সেট ও ফাংশন ২.২।part-02 #ssc

নবম দশম শ্রেণির গণিত অনুশীলনী ২.২ এর ১২,১৩,১৪ ও ১৫ নং প্রশ্নের সমাধান। সেট ও ফাংশন ২.২।part-02 অন্বয়, ডোমেন ও রেঞ্জ—সংজ্ঞা ও বিশ্লেষণ নবম-দশম শ্রেণির সাধারণ গণিত-এ অন্বয় (Mapping), ডোমেন (Domain) ও রেঞ্জ (Range) খুব গুরুত্বপূর্ণ একটি অধ্যায়। এগুলো মূলত ফাংশনের ভিত্তি গঠনে সাহায্য করে। নিচে এগুলোর বিস্তারিত ব্যাখ্যা দেওয়া হলো। ১. অন্বয় (Mapping) কী? একটি সেটের উপাদানকে অন্য সেটের উপাদানের সাথে বিশেষ নিয়মে সম্পর্কিত করা হলে, তাকে অন্বয় (Mapping) বলে। উদাহরণ: ধরা যাক, A = {1, 2, 3} B = {4, 5, 6} এখন যদি প্রতিটি A-এর উপাদানকে B-এর একটি নির্দিষ্ট উপাদানের সাথে সম্পর্কিত করি, তাহলে সেটি অন্বয় হবে। যেমন, যদি অন্বয় হয়— f(1)=4,f(2)=5,f(3)=6f(1) = 4, f(2) = 5, f(3) = 6, তাহলে এটি একটি অন্বয়। অন্বয়ের কিছু গুরুত্বপূর্ণ বিষয় প্রতিটি A-এর উপাদান অবশ্যই B-এর একটি নির্দিষ্ট উপাদানের সাথে সম্পর্কিত হবে। A-এর একটি উপাদান B-এর একাধিক উপাদানের সাথে সম্পর্কিত হলে এটি অন্বয় হবে না। ২. ডোমেন (Domain) কী? ফাংশনের ইনপুট মানগুলোর সেট-কে ডোমেন (Domain) বলে। উদাহরণ: যদি f(x)=x2f(x) = x^2 হয় এবং x-এর মান নেওয়া হয় {1, 2, 3}, তাহলে ডোমেন = {1, 2, 3}। ডোমেন নির্ধারণের নিয়ম: ডোমেনে কেবল সেই মানগুলো থাকবে, যেগুলোর জন্য ফাংশনের মান সংজ্ঞায়িত হয়। যদি কোনো মান বসালে ফাংশন অসম্ভব (Undefined) হয়, তবে সেটি ডোমেনে থাকবে না। উদাহরণ: f(x)=1x−2f(x) = \frac{1}{x-2} এখানে, x=2x = 2 দিলে 0 দ্বারা ভাগ করার সমস্যা হয়। তাই x = 2 ডোমেনে থাকবে না। ৩. রেঞ্জ (Range) কী? ফাংশনের আউটপুট মানগুলোর সেট-কে রেঞ্জ (Range) বলে। উদাহরণ: যদি f(x)=x2f(x) = x^2 এবং ডোমেন = {1, 2, 3} হয়, তাহলে রেঞ্জ = {1², 2², 3²} = {1, 4, 9}। রেঞ্জ নির্ধারণের নিয়ম: প্রতিটি ডোমেনের জন্য নির্ধারিত মানগুলোই রেঞ্জ তৈরি করে। কিছু ফাংশনের জন্য রেঞ্জ নির্দিষ্ট সীমার মধ্যে থাকে, যেমন বর্গমূল ফাংশন (√x) সবসময় ধনাত্মক হয়। সংক্ষেপে গুরুত্বপূর্ণ পয়েন্ট: বিষয়সংজ্ঞাঅন্বয় (Mapping)এক সেটের উপাদানকে আরেক সেটের উপাদানের সাথে সম্পর্কিত করা।ডোমেন (Domain)ফাংশনে ইনপুট হিসেবে ব্যবহৃত সম্ভাব্য উপাদানগুলোর সেট।রেঞ্জ (Range)ফাংশন থেকে প্রাপ্ত আউটপুট মানগুলোর সেট। উদাহরণ ও অনুশীলন প্রশ্ন: যদি f(x)=x+3f(x) = x + 3 হয় এবং x-এর ডোমেন হয় {1, 2, 3, 4}, তাহলে রেঞ্জ কী হবে? সমাধান: f(1)=1+3=4f(1) = 1 + 3 = 4 f(2)=2+3=5f(2) = 2 + 3 = 5 f(3)=3+3=6f(3) = 3 + 3 = 6 f(4)=4+3=7f(4) = 4 + 3 = 7 তাহলে, রেঞ্জ = {4, 5, 6, 7}। উপসংহার অন্বয়, ডোমেন ও রেঞ্জ গণিতের ফাংশন অধ্যায়ের মূল ভিত্তি। এগুলো ভালোভাবে অনুশীলন করলে ভবিষ্যতে জ্যামিতিক বিশ্লেষণ, ক্যালকুলাস ও উচ্চতর গণিতে ভালো দক্ষতা অর্জন করা সম্ভব। সেট ও ফাংশন সম্পর্কে বিস্তারিত আলোচনা: সেট (Set): সেট হলো কিছু নির্দিষ্ট ও সুনির্দিষ্ট উপাদানের একটি সুশৃঙ্খল সংগ্রহ। প্রতিটি উপাদানকে সেটের সদস্য বা উপাদান বলা হয়। সেটকে সাধারণত প্রধান ইংরেজি অক্ষর দিয়ে প্রকাশ করা হয়, যেমন AA, BB, CC। সেটের বৈশিষ্ট্য: নির্দিষ্টতা: একটি সেটে উপাদানগুলো নির্দিষ্ট এবং সুসংজ্ঞায়িত হতে হবে। অন্যুনতা: একটি সেটে কোনো উপাদান একাধিকবার থাকবে না। সেট প্রকাশের পদ্ধতি: Roster বা Listing পদ্ধতি: যেখানে উপাদানগুলো কৌঁচক চিহ্ন { } এর মধ্যে তালিকা আকারে লেখা হয়। উদাহরণ: A={1,2,3,4}A = \{1, 2, 3, 4\} Set-builder পদ্ধতি: যেখানে উপাদানগুলোর বৈশিষ্ট্য প্রকাশ করে সেটটি সংজ্ঞায়িত করা হয়। উদাহরণ: A={x:x হলো ১০-এর কম ধনাত্মক পূর্ণসংখ্যা}A = \{x : x \text{ হলো ১০-এর কম ধনাত্মক পূর্ণসংখ্যা}\} সেটের প্রকারভেদ: শূন্য সেট: কোনো উপাদান না থাকলে সেটটিকে শূন্য সেট বা ফাঁকা সেট বলে। উদাহরণ: A={x:x2=−1}A = \{x : x^2 = -1\} সীমাবদ্ধ সেট: যার উপাদানের সংখ্যা গণনা করা যায়। উদাহরণ: B={1,2,3,4,5}B = \{1, 2, 3, 4, 5\} সীমাহীন সেট: যার উপাদানের সংখ্যা অসীম। উদাহরণ: C={x:x হলো প্রাকৃতিক সংখ্যা}C = \{x : x \text{ হলো প্রাকৃতিক সংখ্যা}\} ফাংশন (Function): ফাংশন হলো দুটি সেটের মধ্যে একটি সম্পর্ক, যেখানে প্রথম সেটের প্রতিটি উপাদান ঠিক একটি নির্দিষ্ট উপাদানের সাথে সম্পর্কিত থাকে। ফাংশনের উপাদান: ডোমেন (Domain): প্রথম সেটের উপাদানগুলো। কোডোমেন (Codomain): দ্বিতীয় সেটের উপাদানগুলো। ইমেজ (Image): কোডোমেনের সেই উপাদান যা ডোমেনের উপাদান দ্বারা সম্পর্কিত। সেট ও ফাংশন নবম দশম শ্রেণির সাধারণ গণিত অনুশীলনী ২.২ সেট ও ফাংশন ২.২ দশম শ্রেণির গণিত ২.২ নবম দশম শ্রেণির গণিত সেট ও ফাংশন সেট ও ফাংশন ২.২এর সমাধান অনুশীলনী ২.২এর সমাধান class 10 math 2.2 class ten math 2.2 Class x math 2.2 Set and function class 10 Set and function 2.2 Ssc math 2.2 নবম দশম শ্রেণির গণিত অনুশীলনী ২.১ এর ১২ নং প্রশ্নের উত্তর। নবম দশম শ্রেণির গণিত অনুশীলনী ২.১ এর ১১ নং প্রশ্নের উত্তর Class x math chapter 2.1 exercise 11,12 Class ten math chapter 2.2 exercise 12,13,14,15 নবম দশম শ্রেণির সাধারণ গণিত অনুশীলনী ২.২ এর ১২ নং প্রশ্নের সমাধান। নবম দশম শ্রেণির সাধারণ গণিত অনুশীলনী ২.২ এর ১৩ নং প্রশ্নের সমাধান। নবম দশম শ্রেণির সাধারণ গণিত অনুশীলনী ২.২ এর ১৪ নং প্রশ্নের সমাধান। নবম দশম শ্রেণির সাধারণ গণিত অনুশীলনী ২.২ এর ১৫ নং প্রশ্নের সমাধান। #নবমদশমশ্রেণি #গণিত #সেটওফাংশন #অনুশীলনী২_২ #গণিতসমাধান #বাংলাগণিত #শিক্ষা #শিক্ষামূলকভিডিও #EduEnrichWithEmon #বাংলাটিউটোরিয়াল #গণিতশিক্ষা #SSCPreparation #MathSolutions #SetAndFunction #MathTutorial #সাধারণগণিত #বাংলাদেশশিক্ষাবোর্ড #SSCExam #গণিতশিক্ষক #অনলাইনশিক্ষা #MathPractice #BanglaEducation #SSC2024 #SSC2025 #StudentHelp #MathLecture #মাধ্যমিকগণিত #অনুশীলন #ফাংশনসমাধান #Mathematics #SetTheory #FunctionTutorial #SSCStudents #EducationForAll #OnlineLearning