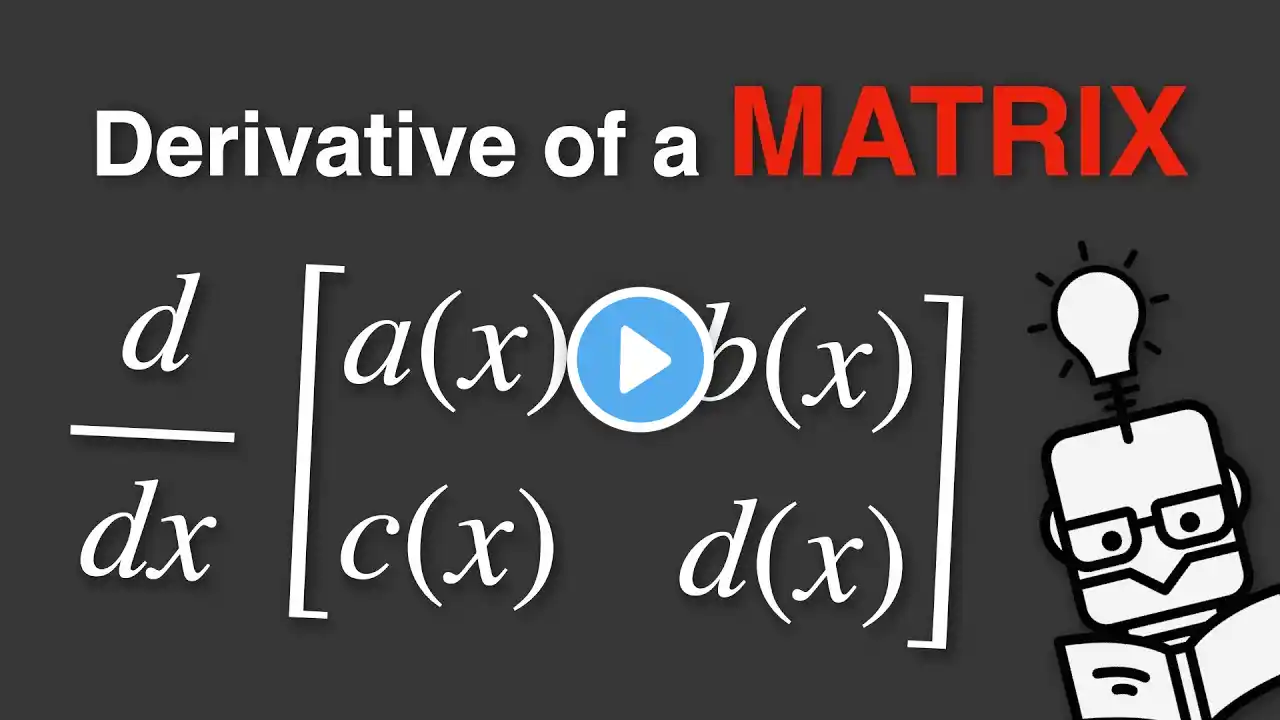
Derivative of a Matrix - Explained
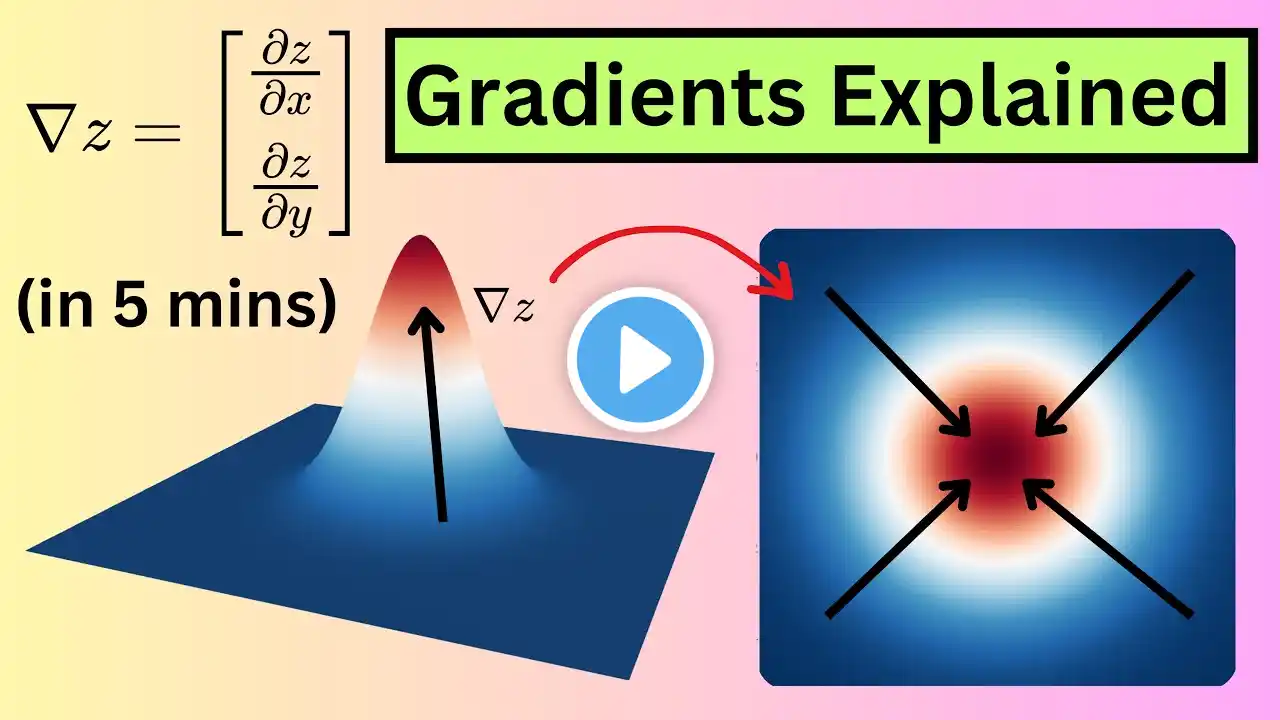
This video explains matrix calculus by computing derivatives of functions involving matrices, focusing on linear maps and quadratic forms. It shows how the derivative of a matrix-vector product leads to the Jacobian matrix, and how the gradient of a quadratic form results in a simple matrix expression. These results are directly connected to scalar calculus and are fundamental for machine learning, optimization, linear algebra, and applied mathematics. Related Videos ▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬ The Hessian Matrix: • The Hessian Matrix - Explained The Jacobian Matrix: • The Jacobian Matrix - Explained Bayesian Optimization: • Bayesian Optimization Hyperparameters Tuning: Grid Search vs Random Search: • Hyperparameters Tuning: Grid Search vs Ran... The Kernel Trick: • The Kernel Trick Cross-Entropy - Explained: • Cross-Entropy - Explained Dropout - Explained: • Dropout in Neural Networks - Explained Overfitting vs Underfitting: • Overfitting vs Underfitting - Explained Why Models Overfit and Underfit - The Bias Variance Trade-off: • Bias-Variance Trade-off - Explained Least Squares vs Maximum Likelihood: • Least Squares vs Maximum Likelihood Contents ▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬ 00:00 - Intro 00:13 - Scalar calculus recap 00:35 - Linear form 01:50 - Quadratic form 03:13 - Summary 03:42 - Outro Follow Me ▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬ 🐦 X: @datamlistic https://x.com/datamlistic 📸 Instagram: @datamlistic / datamlistic 📱 TikTok: @datamlistic / datamlistic 👔 Linkedin: / datamlistic Channel Support ▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬ The best way to support the channel is to share the content. ;) If you'd like to also support the channel financially, donating the price of a coffee is always warmly welcomed! (completely optional and voluntary) ► Patreon: / datamlistic ► Bitcoin (BTC): 3C6Pkzyb5CjAUYrJxmpCaaNPVRgRVxxyTq ► Ethereum (ETH): 0x9Ac4eB94386C3e02b96599C05B7a8C71773c9281 ► Cardano (ADA): addr1v95rfxlslfzkvd8sr3exkh7st4qmgj4ywf5zcaxgqgdyunsj5juw5 ► Tether (USDT): 0xeC261d9b2EE4B6997a6a424067af165BAA4afE1a #matrixcalculus #linearalgebra #machinelearning #optimization #math