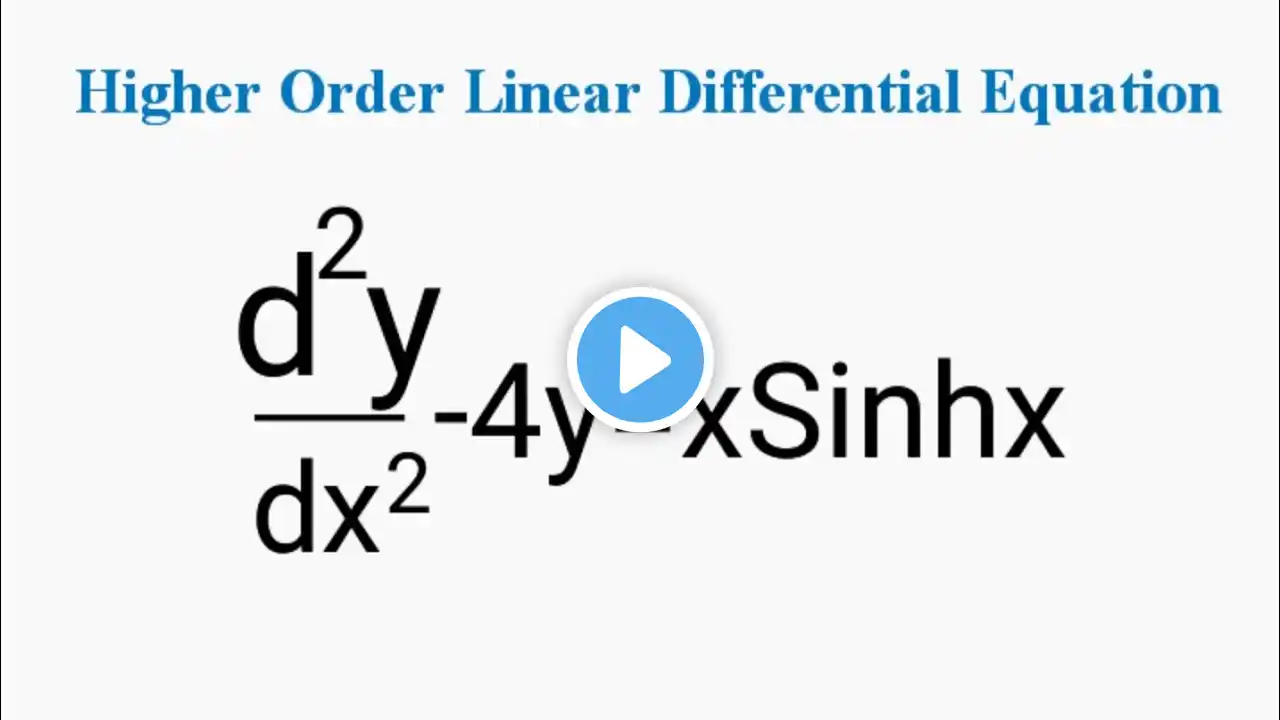Higher Order Differential Equation | (D³ − D² + 4D − 4)y = sinh(2x+3) | C.F. & P.I. Solution

Solution of (D³ − D² + 4D − 4) y = sinh(2x + 3) (For BMATE301 / BEE301 – Module 1, BMATEC301 / BEC301 – Module 4) (2025 Scheme – 1BMATE101 / 1BMATC101 – Module 4) (2022 Scheme – BMATM101 / BMATC101 – Module 4) Step 1 – Auxiliary equation: m³ − m² + 4m − 4 = 0 Step 2 – Factorize: (m − 1)(m² + 4) = 0 Step 3 – Roots: m = 1, m = ± 2i Step 4 – Complementary function (C.F.): m = 1 → eˣ m = ± 2i → cos(2x), sin(2x) C.F. = C₁ eˣ + C₂ cos(2x) + C₃ sin(2x) Step 5 – Particular integral (P.I.): For RHS sinh(2x + 3) → write as (e^(2x+3) − e^(−2x−3))/2 and solve using operator method. Step 6 – General solution: y = C₁ eˣ + C₂ cos(2x) + C₃ sin(2x) + (P.I. term) #HigherOrderDifferentialEquations #EngineeringMathematics #VTU #BMATE301 #BEE301 #BMATEC301 #BEC301 #BMATM101 #BMATC101 #2025Scheme #2022Scheme #DifferentialEquations #ComplementaryFunction #ParticularIntegral #HyperbolicFunctions #Sinh #Cosh #AuxiliaryEquation #Roots #MathsForEngineers #VTUMaths #MathTutorial #SolveDE #MathsSolution #MathLecture #MathStudy #MathTricks #MathProblemSolving #LearnMaths #MathematicsTutor #MathClasses