Mid Point Theorem Used by Architects | Quadrilaterals | CBSE Class 9 | Episode 5 | Genius Maths

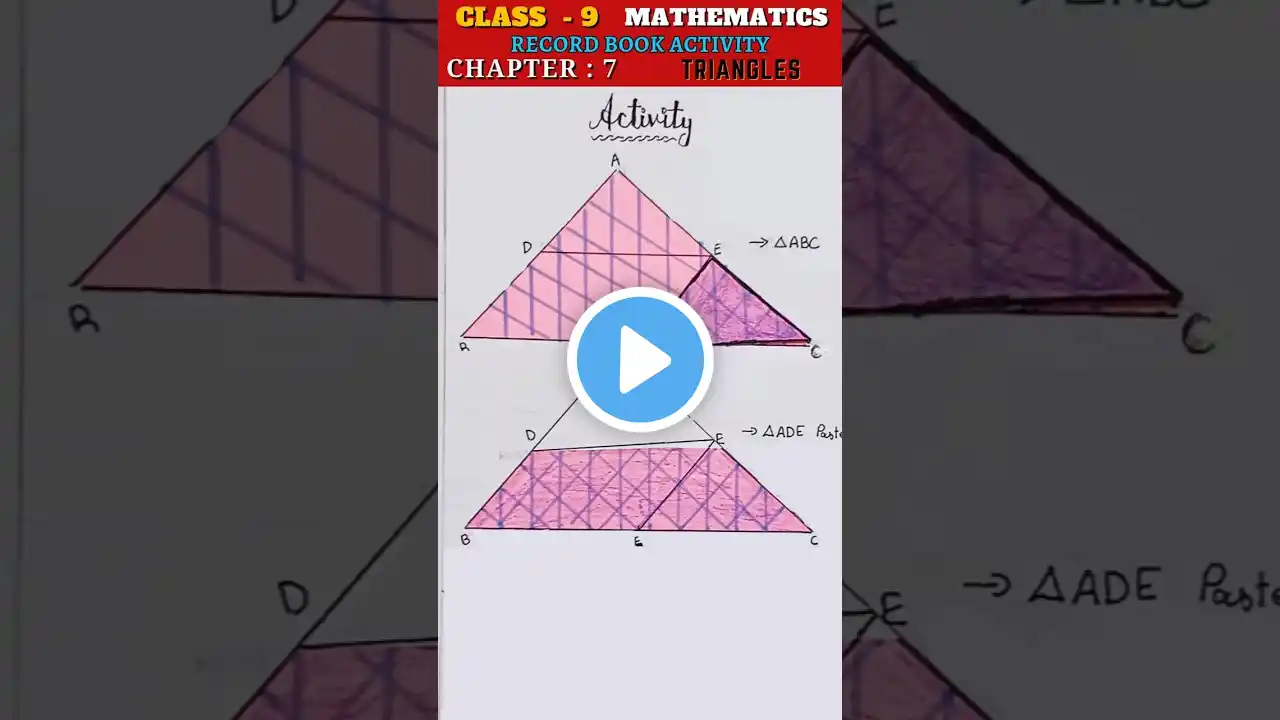
In this Genius Teacher video you will learn about "What are Quadrilaterals?","What are types of quadrilaterals?" and much more about Maths Chapter 8, Quadrilaterals for CBSE Class 9 explanation made easy and interesting to learn for kids in Hindi using examples from beautiful architectures around the world! At the end of this video, students will be able to: 🔍Learn about Quadrilaterals 🔍Learn about types of quadrilaterals 🔍Learn about vertices, sides and angles of a quadrilateral 🔍Learn about properties of quadrilaterals 🔍Learn about properties of parallelograms 🔍Learn about properties of rectangle 🔍Learn about properties of square 🔍Learn about properties of rhombus 🔍Learn about mid point theorem Stay tuned for more episodes on CBSE Maths Class 9 Chapter 8 Quadrilaterals. Take Genius Quizzes on Class 9 Maths Quadrilaterals NCERT syllabus on GeniusApp linked below. ⭐ Get it on Google Play - https://play.google.com/store/apps/de... ⭐ Play Quiz on Genius Web App - https://app.geniusteacher.in/student/ ⭐ Follow us on Instagram -   / geniusteach.  . ⭐ Follow us on Facebook -   / geniusteachers   Watch other Genius: Maths videos: 📌Number System| Class 9| Episode 1|-   • what are the Types of Number Systems? | CB...   📌Number System| Class 9| Episode 2|-    • how to represent Real Numbers on Number Li...   In this genius video, you will learn how architects and designers used the mid-point theorem to design this stunning piece of architecture in China - the Shenzhen Universiade Sports Centre. Every facet of the exterior of this exclusive sports centre is triangular. Therefore to provide it with the best possible support, the architects used the mid-point theorem. They placed the support beam at PQ where P was the midpoint of side AB and Q was the midpoint of side AC By using the midpoint theorem we can prove that PQ is parallel to BC and also PQ is equal to half the length of BC. "Extend the line segment PQ upto R such that, PQ=QR like this "In the triangle APQ, and triangle CRQ AQ= QC" and ∠AQP = ∠CQR because they are vertically opposite angles "and PQ = QR therefore both these triangles - that is - triangle APQ, and triangle CRQ are congruent triangle by the SAS test" "Therefore, the corresponding angles ∠PAQ and ∠RCQ will also be equal Now observe that CR and AB are two lines which are intersected by the transversal AC, then these angles ∠PAQ and ∠RCQ are alternate angles. And what happens if the alternate angles are equal? (pause) The two lines are said to be parallel lines. Therefore, line CR is parallel to AB or CR is parallel to PB" "Similarly, the corresponding sides CR and AP are also equal But, P is the midpoint of AB. So AP = PB = CR" Therefore it follows that quadrilateral PBCR is a parallelogram. "And what do we know about parallelograms? That the opposite sides are parallel and equal." Therefore PR is parallel to BC or we can also say that PQ is parallel to BC. "Also, since its a parallelogram, PR is equal to BC But PR = PQ + QR Therefore we can say that BC = PQ + QR Also PQ = QR Therefore, BC = 2PQ or PQ = 1/2 BC" Thus we have proved the midpoint theorem which states that "The line segment joining the mid-points of two sides of a triangle is parallel to the third side" which means that if P and Q are the midpoints of AB and AC then PQ is parallel to BC Similarly, we can also prove the converse of this theorem which states that "The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side." So if P is the midpoint of AB and line PQ is parallel to BC, then we can say that Q is the midpoint of AC So, now that you know the mid-point theorem, you can easily see, how architects use their basic knowledge of geometry to provide support to stunning pieces of architecture.